Notes (HPFP 06/31): Typeclasses

6 Typeclasses

6.2 What are typeclasses?

“Typeclasses and types in Haskell are, in a sense, opposites”.

Sentences like these frustrate me. You can say nearly anything is the case “in a sense:”

“In a sense, the Moon really is made of cheese.” In the sense of poetic whimsy.

“In a sense, Johnny is at the top of his class.” In the sense of unexcused absences and missed assignments.

“In a sense, types and typeclasses are the same.” In the sense that they both specify and constrain the properties of expressions.

“In a sense, types and typeclasses are opposites.” In the sense that generation is opposed to consumption. The type definition is where you figure out how to make values; the typeclass definition is where you write interfaces that can use those values.

If an expression’s type is an instance of Eq it means there’s a way to define to define and equals function (==) to check if two expressions of that type are equal:

Prelude> :info Eq
class Eq a where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool
  {-# MINIMAL (==) | (/=) #-}
    -- Defined in ‘GHC.Classes’

But there are types that it is impossible to define (==) for! The function constructor (->), for example, cannot be an instance of Eq. Why? The Halting Problem! If there’s no general way to test whether a function will halt on a given input, there’s certainly no general way to determine whether two functions will do the same thing (run forever or return the same value) for a given input.

So typeclasses constrains the potential things types can be by specifying what they can do.

Some typeclasses and their relationships:

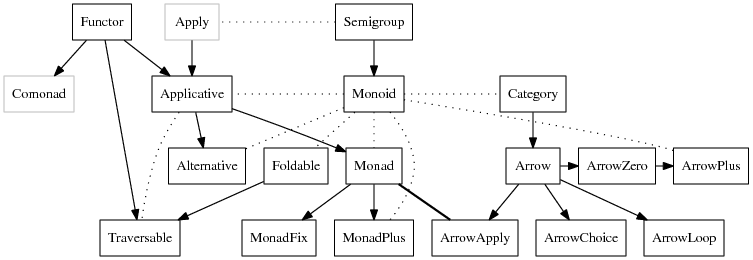
Typeclassopedia

6.5 Writing typeclass instances

The thing about writing your own instances vs deriving them automagically is that when you write your own you have control over what the instance does, whereas GHC can only derive them in one way.

For example, if I using the automatic deriving for the typeclass Show:

> data Foo = Foo deriving Show
> show Foo
"Foo"

GHC derives the show function so that the output string is just whatever the data constructor is.

But it doesn’t have to be! We could manually write a perfectly valid Show instance for Foo like so:

> data Foo = Foo
> instance Show Foo where show Foo = "Bar"
> show Foo
> "Bar"

All we need for a Show, is a show :: a -> String function, but there are no promises as to what String is shown!

Partial functions

total function: a functional that is defined for all inputs in its domain. partial function: a function that is undefined for some inputs in its domain.

The -Wall compiler flag means “Warnings, all”. It’s a common pattern for compiler flags that deal with warnings to begin with “W”.

Exercises: Eq Instances

see EqInstances.hs

Exercises: Tuple Experiment

quotRem and divMod return a tuple with the values from quot and rem or div and mod respectively.

Exercises: Will They Work?

  1. 5
  2. LT
  3. error, a string and a bool are not comparable
  4. False

Chapter Exercises

Multiple choice

  1. c
  2. b
  3. a
  4. c
  5. a

Does it typecheck?:

see Exercises.hs

Given a datatype declaration, what can we do?

see Datatype.hs

Match the types:

  1. Since i = 1, i has to be a Num, it can’t be a type that 1 isn’t, like e.g. a String. We can’t cast i upwards.
  2. 1.0 is not just any instance of Num, the syntax implies Fractional.
  3. works
  4. works
  5. works, we can always cast downwards
  6. works
  7. Doesn’t work, sigmund returns myX which is an Int
  8. Doesn’t work, sigmund' returns an Int not any instance of Num
  9. Works, restricts jung to a list of Ints rather than any list
  10. Works, restricts input to String
  11. Doesn’t work, mySort only sorts Strings, not any instance of Ord

Type-Kwon-Do: Electric Typealoo

see TypeKwonDo.hs

6.17 Follow-up resources

  1. P. Wadler and S. Blott. How to make ad-hoc polymorphism less ad hoc.

  2. Cordelia V. Hall, Kevin Hammond, Simon L. Peyton Jones, and Philip L. Wadler. Typeclasses in Haskell.